Avid readers will of course remember the review of
Larry Niven's Ringworld, posted by Roh earlier this year (8 months ago, in fact. Where did all that time go?). In a comment, I briefly mentioned that the physics of the Ringworld concept mostly seemed sound, but I didn't go into detail. Today, however, I am going to do just that, in respons to a request by Tim a few weeks back. I'm sorry for the delay, and I hope you didn't figure it out for yourself in the meantime.
In calculating the apparent gravity felt by a person standing on the inside surface of a Ringworld, we need to know two things: the radius, and the rotational speed. According to the wikipedia article on
Ringworld, the Ringworld has a radius of 150 million kilometers (pretty much the same as the distance from the Earth to the Sun), and makes a complete orbit in 225 hours, meaning it rotates at the ridiculous speed of
When we know the radius and the speed, we can calculate the apparent gravity from the formula for centripetal acceleration:
In other words, the inhabitants of the Ringworld would feel about 10% less gravity than we do on Earth. In the case of the Orbitals of Iain Banks' Culture series, which, now that I think about it, is what Tim's question actually referred to, the maths is the same. A typical Orbital has, again according to wikipedia, a radius of 3 million kilometers. The rotational period, however, does not seem to be specified. Still, we can assume that the gravity is to be roughly the same as on Earth, and work out the orbital peroid from that:
To sum up, the equation relating the radius, the rotational period and the apparent gravity of a Ringworld-like structure is
Naturally, such structures would have to be built from extremely strong materials, far surpassing anything known today. Interestingly, in the case of the Ringworld, the material is described as having some properties in common with nuclear material. If it also had the density of nuclear material, the gravity from the ring itself would be millions of times greater than the apparent gravity produced by rotation.
-Tor Nordam


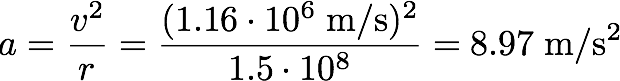
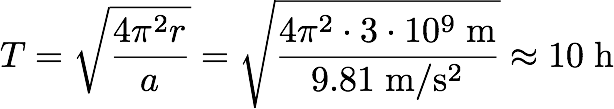
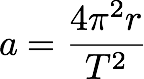
Comments